It is an efficient [1] MC method which can be applied to problems where important regions (e.g. transition states) of the energy landscape may be difficult to sample with a standard random walk method, such as Metropolis sampling.
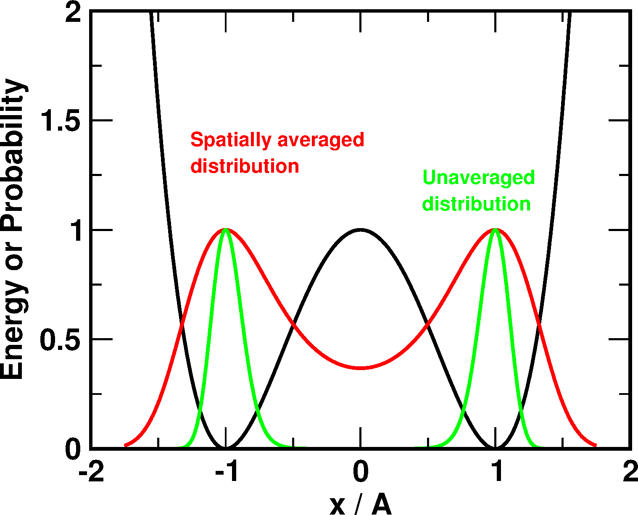
At the heart of the method is the realization that from the equilibrium density a related, modified probability density can be constructed through a suitable transformation. This new density is more highly connected which increases the chances for transitions between neighboring states which in turn speeds up the sampling. In order to transform the equilibrium density, Gaussian distributions with variable widths are used.

First successful investigations included the diffusion of small molecules in condensed phase environments [2,3] and localization of lowest energy structures of Lennard-Jones clusters [3,4]. A more general implementation in CHARMM allowed us to study the conformation space of biomolecules [4].
![Free energy surface based on ramachandran plots obtained using: [A] MD, [B] MC, [C and D] SA-MC, respectively biased and unbiased.](https://fhedin.com/wp-content/uploads/2019/06/samc-fe-1024x901.jpg)
[1] JD Doll, JE Gubernatis, N Plattner, M Meuwly, P Dupuis, and H Wang, J. Chem. Phys. 2009, 131.
[2] N Plattner, JD Doll, and M Meuwly, J. Chem. Phys. 2010, 133.
[3] F Hédin, Master Thesis, Université de Strasbourg & Universität Basel 2011.
[4] F Hédin, N Plattner, JD Doll and M Meuwly, J. Chem. Theory Comput., 2014.